Computational Science
Many challenges in civil engineering involve multi-physics problems, where not just one, but multiple physical and chemical phenomena—such as the mechanics of solids, liquids, and gases, the transport of mass and heat, and chemical reactions—occur simultaneously.
We address these complex multi-physics problems in civil engineering through a wide range of approaches, from the development of fundamental theories to advanced, high-accuracy, and large-scale numerical computation techniques.
Our research spans from developing material models that describe intrinsic properties, formulating governing equations by combining the relevant physical laws, implementing these models into numerical simulations, and applying them to real-world and large-scale engineering problems. We also actively conduct laboratory experiments and field measurements as part of the model validation and refinement process.
At the core of our research is the challenge of describing complex multi-physics phenomena using the fewest and most essential assumptions possible.
Academic Staff
Mamoru KIKUMOTO
Professor (Academic Center for Computing and Media Studies)
Research Topics
My research focuses on the development of fundamental models and simulation techniques for geomaterials such as soil and rock. To ensure the reliability of our models and numerical methods, we also conduct laboratory experiments and field measurements in parallel.
Geomaterials are complex and fascinating substances composed of a mixture of solid, liquid, and gas phases. Due to their complex behavior, conventional theories and computational techniques often fall short in accurately predicting their responses.
To overcome these limitations, we are developing new models and simulation techniques capable of describing the mechanical and hydraulic behavior of geomaterials. In addition to validating these methods, we are also working on applying them to high-precision and large-scale numerical analyses using the supercomputing facilities at the Academic Center for Computing and Media Studies.
Contacts
Room 219, Research Bldg. No.5, Yoshida Campus, Kyoto University, Yoshida Honmachi, Sakyo-ku, Kyoto 606-8501, Japan
TEL: +81-75-753-7493
E-mail: kikumoto.mamoru.6x![]() kyoto-u.ac.jp
kyoto-u.ac.jp
Research Topics
Modeling of Geomaterials
Geomaterials are mixtures of solids, liquids, and gases, and exhibit unique, complex behavior. We aim to overcome the limitations of conventional geomechanics by developing theoretical models that can reliably predict such behavior. Our research philosophy follows Occam’s Razor: the problem-solving principle that recommends searching for explanations constructed with the smallest possible set of elements. Based on this principle, we are developing rational models that capture the responses of geomaterials with a minimal number of simplified assumptions.

Fig. 1. 3D state boundary surface capturing evolving grading.
Micro-Macro Transition of Granular Media
To develop rational models, it is essential to understand how micro-level interactions between particles govern macro-scale mechanical response. We are investigating the micro–macro linkage by combining laboratory testing with granular mechanics simulations, aiming to uncover the intrinsic mechanical properties of granular materials.
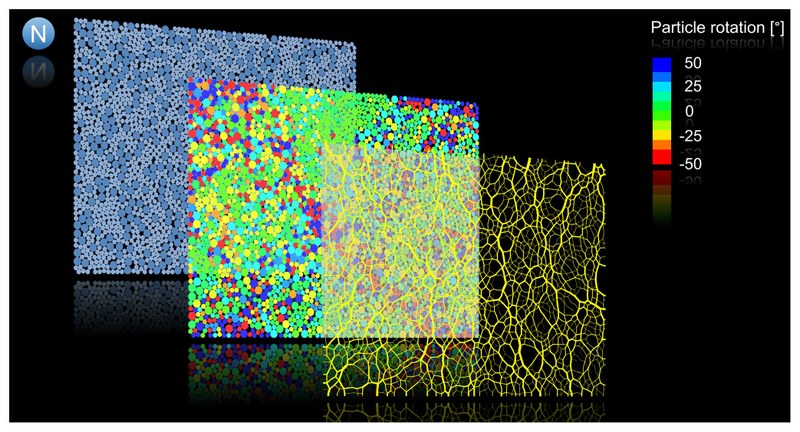
Fig. 2. Simulation of micro-macroscopic granular behavior
From Empirical Knowledge to Rational Science
Our objective is to transform mechanical understanding from empirical knowledge into theory-based science. We focus on earth structures such as tunnels and cut slopes, integrating lab tests, field surveys, modeling, and simulations. In particular, we are developing a method to predict rock weathering and assess the long-term stability.


Fig. 3. Weathering of weak rocks and simulation of instability of cut slope.
Geoenvironmental Geotechnics and Interdisciplinary Research
We work on environmental geotechnics, focusing on soil contamination caused by oil and heavy metals. This includes the development of fundamental physical models and advanced simulations. In addition, we actively engage in interdisciplinary research, collaborating with experts in cultural heritage preservation and other fields.


Fig. 4. Simulation of soil contamination using oil–water–air multiphase flow analysis.


Fig. 5. Laboratory investigation of tunnel-masonry interaction.
