Applied Mechanics
The most important thing for the development of infrastructures is to ensure their safety quantitatively from the standpoint of mechanics at all the steps, such as planning, design, construction and management. To this end, we carry out researches on the fundamental mechanics and its application. Simultaneously, we will educate and nurture the young researchers who are able to inherit and spread fruitful results of Engineering Science.
As far as studies on the applied mechanics are concerned, the most important thing is to construct a simple model of mechanical behavior as long as the observed data in site investigations or model tests are rationally explained. To carry out these researches, fundamental knowledge of mathematics and mechanics is requisite. We also attach weight to education of these subjects to younger generations.
Academic Staff
Abbas KHAYYER
Associate Professor (Graduate School of Engineering)
Research Topics
Our final target is to develop an accurate and efficient multi-physics particle-based solver for Coastal/Offshore Engineering applications. The following key steps will be taken to achieve this goal: 1) Development of consistent, conservative and highly accurate particle-based numerical schemes from a physical-mathematical view point 2) Enhancement of computational efficiency by parallelization and GPU-based computations 3) Incorporation of accurate sub-models (e.g. turbulence models) for a more reliable simulation of complex physics 4) Development of multi-physics models to account for the fluid-structure-soil interactions.
Contacts
Room 585, Bldg. C1, Katsura Campus
TEL: +81-75-383-3180
FAX: +81-75-383-3183
E-mail: khayyer particle.kuciv.kyoto-u.ac.jp
particle.kuciv.kyoto-u.ac.jp
Jun SAITO
 Associate Professor (Graduate School of Engineering)
Associate Professor (Graduate School of Engineering)
Research Topics
I investigate finite element method and optimal design to develop a tool for supporting design of structures. Simultaneously, I am interested in the mechanical behavior of the underground structures.
Contacts
Room 586, Bldg. C1, Katsura Campus
TEL: +81-75-383-3181
FAX: +81-75-383-3183
E-mail: saito.jun.3n kyoto-u.ac.jp
kyoto-u.ac.jp
Research Topics
Lagrangian particle methods for fluid flow simulations
The so-called particle methods are appropriate candidates for fluid flow simulations in view of their flexibility and potential robustness in dealing with highly-deformed convection-dominated problems. However, since particle methods are relatively new computational techniques, there have been several issues corresponding to non-exact momentum/energy conservation, unphysical pressure fluctuations and numerical instability. In this regard, significant improvements have been achieved. The main ongoing/future researches are focused on:
- further enhancement of accuracy and stability of particle methods by development of further accurate, consistent and conservative numerical schemes/algorithms
- further enhancement of the developed multiphase gas-liquid particle-based method by a meticulous modeling of the governing physics
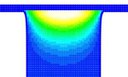
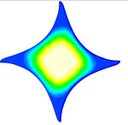

Figure 1. Water jet impact, fluid patch evolution, air-water multiphase sloshing
Particle-based Fluid-Structure Interactions
Fluid Structure Interaction (FSI) is of significant relevance in many fields of engineering as well as applied sciences. A reliable FSI simulation requires accurate Computational Fluid Dynamics (CFD) and Computational Structural Dynamics (CSD) models as well as a meticulously consistent coupling approach. Our research is focused on development of a reliable particle-based FSI solver by incorporating accurate fluid and structure models as well as a mathematically-physically consistent algorithm for their coupling.
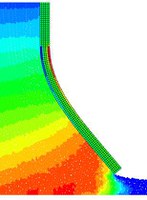
Figure 2. Dam break flow through an elastic gate
Mathematical structure of limit / shakedown analysis and its numerical simulation method
Metal forming, bearing capacity and slope stability problems are sometimes treated as rigid-plastic boundary value problems, because elastic deformation is small and negligible in comparison with plastic deformation. Limit analysis is well known as a mighty basis to solve such kinds of problems. Rigid plastic finite element method (RPFEM) based on the upper bound method is widely used as a powerful numerical tool for these problems. On the other hand, the lower bound method which is dual to the upper bound method is rarely used. In this study, in order to utilize the duality of limit analysis, a hybrid type rigid plastic finite element method which combines both the primal problem (the lower bound method) and the dual problem (the upper bound method) together, is newly formulated from the standpoint of nonlinear optimization theory. In addition to this, applicability of similar methodology to shakedown analysis which can be recognized as a generalization of limit analysis is investigated.
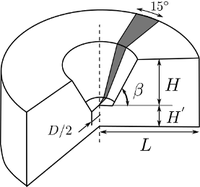
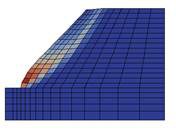
Figure 3. Stability Analysis of excavation
Research on non destructive evaluation using ultrasound and laser measurement
Techniques to detect small defects are important in evaluating the safety of structures. Especially important is the ultrasonic testing which is safe and practical. Unfortunately, however, only a small part of the abundant information of the ultrasonic measureme nt is used in practice because the output of ultrasonic transducers used in the ultrasonic testing is hard to interpret physically.

Figure 4. Scattered waves from a surface crack.
Comparison of the real data of the laser velocimetry and the simulated results.
Hence in our laboratory, we measure the particle velocities of ultrasounds with a laser interferometer to analyze the characteristics of the ultrasonic transducer and then utilize the results in a quantitative ultrasonic nondest ructive evaluation of determining the shapes and locations of defects.
